Theory

A 2d Delaunay triangulation (DT) for a set P of points in the plane is a triangulation such that no point in P is inside the circumcircle of any triangle in the triangulation. It can be shown that for all possible triangulations of P, a Delaunay triangulation maximizes the minimum angle of all angles of the triangles in the triangulation.

Thus, a Delaunay triangulation tends to avoid “skinny” triangles. This property makes it the triangulation of choice for many purposes, including Digital Terrain Modelling (DTM). 

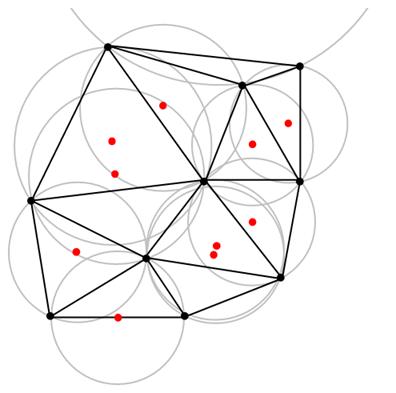
Figure 31: A Delaunay triangulation with all circumcircles and their centres. Image available under GNU license at http://en.wikipedia.org/wiki/File:Delaunay_circumcircles_centers.png

A Delaunay triangulation is unique in a general case. It is not unique if four triangulation points lie on the same circle.

A 2d conforming Delaunay triangulation (CDT) is a Delaunay triangulation that respects constraints (edges). This is done by iteratively inserting additional points (called Steiner points) until no triangle crosses a constraint.

Computational power

In general, triangulating pure point data is much faster than triangulation pure constraint data. This is because constraints are processed iteratively until no constraint crosses a triangle. Benchmarks for pure constraint data cannot be given because the number of iterations depends on the distribution of the constraints.

On an average 32bit machine, ComputationalCAD for AutoCAD triangulates about 0.5M to 1M points in about one minute. This may extend to several millions of points on a 64bit machine. The computational complexity is 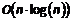, resulting in near-linear computation time over the number of triangulation points. However, the maximum number of triangulation points is limited by the available amount of memory. 

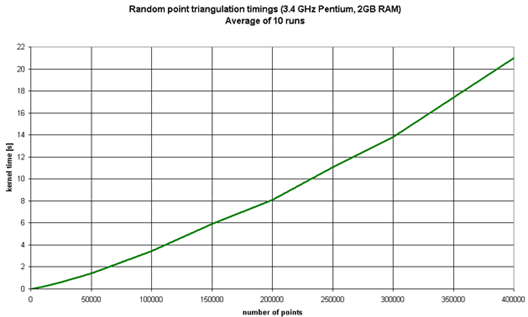
Figure 32: Triangulation timings